WebGPU教程(说人话)绘制一个3D立体动画(三)
作者:秋了秋 发表时间:2024年03月19日
前面的章节用人话讲述了我们怎么使用WebGPU绘制2D图形,总结下它跟canvas 2D画图有什么区别,canvas 2D是JS在CPU里面绘图,CPU是单线程的,WebGPU是在GPU里面画图的,有成千上万的线程,速度上它会非常快。WebGPU除了绘制图形快之外,它还能轻松地画3D立体图形,这是canvas 2D所不具备的,所以3D渲染才是WebGPU的终极武器。
还记得前面第一章节说的3D绘图原理吗,今天复习一下:
"3D其实质在屏幕上都是2D像素,GPU只是把部分顶点通过矩阵运算调整坐标,每一个角度看过去不同的坐标布局,让整体看上去近大远小,再通过远近着不同的深浅明暗颜色,看起来具有纵深感,在人眼视觉上呈现3D的感觉(说人话:相机原理)"
明白原理后,结合之前绘制2D图形的经验,我们只需要稍微改造下代码,有几个额外的步骤需要补上即可:
1. 提供立体图形的所有顶点,上、下、左、右、前、后六个面看过去的构成面的顶点数据。
2. 使用矩阵运算重新计算需要展示的角度看过去的各个顶点的坐标。
3. 配置管线配置primitive的cullMode模式为’back’;
其中1和2是关键步骤,3只是视觉上的优化,背对视角的顶点不渲染。接下来对这三个步骤逐一讲解。
一:3D顶点数据
本文以一个最简单的立方体为例子,告诉你立方体的顶点数据怎么获取,比如我们要使用triangle-list模式绘制,这意味着我们需要提供三角形化的顶点给GPU,一个四方体有6个平面,每个平面由一个矩形构成,每个矩形有两个三角形构成,每个三角形有三个顶点构成,所以一个立方体有6*2*3=36个顶点,每个顶点包含三个值x、y、z,所以一共有36*3 = 108个数据。之前绘制2D不用提供z值,都用1默认补上,3D则必须提供每个顶点的z值才能体现这个点是在前面还是后面(正数、负数)和在后面有多远(0~1)。
复杂的立体图形的顶点是脑补不出来的,需要借助建模软件导出来或者从网上下载,简单的还是可以的,现在我们来脑补一个四方体的顶点,其实构成四方体的2*6=18个三角形的所有顶点坐标只需要8个(正面矩形的4个角和背面矩形的4个角,本文定义从左顶点开始逆时针)顶点,所有三角形只需要复用这8个顶点即可,我们先把这8个顶点定义好:
const vertexMap = [ // 正面 [-0.2,0.5,0.3], [-0.2,-0.5,0.3], [0.2,-0.5,0.3], [0.2,0.5,0.3], // 背面 [0.2,0.5,-0.3], [0.2,-0.5,-0.3], [-0.2,-0.5,-0.3], [-0.2,0.5,-0.3] ];
再来找出每个面的三角形的顶点排列顺序,这个顶点我们先用vertexMap的索引代替,按照逆时针的顺序:
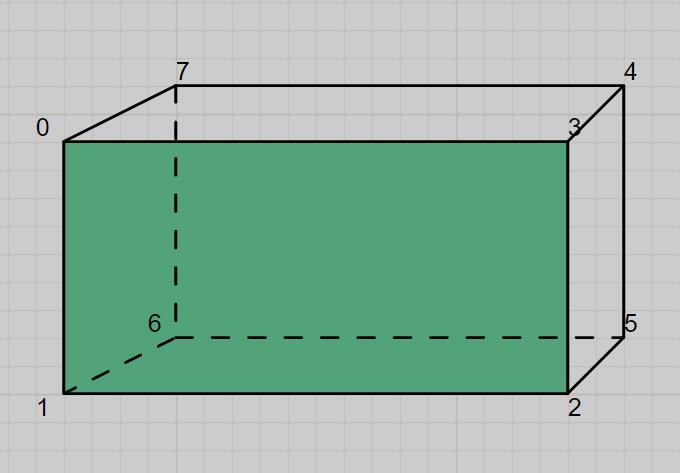
const triangleIndex = [ 1,2,3,1,3,0, //正面 5,6,7,5,7,4, //背面 6,1,0,6,0,7, //左面 2,5,4,2,4,3, //右面 0,3,4,0,4,7, //上面 6,5,2,6,2,1 //下面 ];
最后把它们组装成一个完整的顶点数据并写入vertexBuffer:
let allVertex = triangleIndex.map(index => {
return vertexMap[index];
}).reduce((arr, v)=>{
return arr.concat(v);
});
allVertex = new Float32Array(allVertex);
const vertexBuffer = device.createBuffer({
size: allVertex.byteLength,
usage: GPUBufferUsage.VERTEX | GPUBufferUsage.COPY_DST
});
device.queue.writeBuffer(vertexBuffer, 0, allVertex);
至此,顶点数据就全部准备好了!
二:矩阵调整坐标
我们需要先引入一个工具函数,这个工具函数通过传入不同的角度可以算出基于x或y或z不同角度的4x4矩阵出来:
// 创建旋转矩阵函数
function createRotationMatrix(radians, axis) {
const sin = Math.sin(radians);
const cos = Math.cos(radians);
const omcos = 1.0 - cos;
const x = axis[0], y = axis[1], z = axis[2];
return [
cos + x * x * omcos, y * x * omcos + z * sin, x * z * omcos - y * sin, 0,
x * y * omcos - z * sin, cos + y * y * omcos, y * z * omcos + x * sin, 0,
x * z * omcos + y * sin, y * z * omcos - x * sin, cos + z * z * omcos, 0,
0, 0, 0, 1
];
}
函数计算的原理不在本文探讨,一般也不会手写,直接引入进来就好,有兴趣的可以深入研究,原理就是三角函数的利用。
比如我们需要看绕y轴旋转0.5弧度的立体图形,那它对应的矩阵就是:
let rotateMatrix = createRotationMatrix(0.5, [0,1,0]);
之后所有顶点乘以这个矩阵就是视觉应该看到的新的坐标。很显然这个rotateMatrix 是在CPU定义的,我们需要传入到GPU,变量写入GPU跟顶点数据写入GPU是相类似的,但是它多了一些步骤,具体有:
1. CPU改变变量的值;
2. Device里面createBuffer一个uniform类型的存储空间;
3. 把变量的值writeBuffer进存储空间;
4. createBindGroup创建绑定组;
5. setBindGroup绑定组到GPU;
6. WGSL里面读取使用变量;
第二步:
const matrixBuffer = device.createBuffer({
size: 4 * 16, // matrix 4x4
usage: GPUBufferUsage.UNIFORM | GPUBufferUsage.COPY_DST
});
第三步:
rotateMatrix = new Float32Array(matrix); device.queue.writeBuffer(matrixBuffer , 0, rotateMatrix .buffer, 0, rotateMatrix.byteLength);
需要把rotateMatrix 转成float32格式数据,然后把它的buffer偏移0从头写入matrixBuffer里面。writeBuffer第一个参数是容器,第二个参数是容器存储的偏移量,只存一个数据无特殊需求就是0,第三个参数是要写入的数据,第四个参数是数据本身的偏移值,如果要整个数据,无特殊需求就是0,第五个参数是要写入数据的长度。
第四步:
设置绑定组的作用就是传递数据到GPU,支持批量:
const bindGroup = device.createBindGroup({
layout: pipeLine.getBindGroupLayout(0), // 这个0对应第五步的第一个参数和第六步里面的@group(0)
entries: [
{
binding: 0, // 这个0对应第六步里面的@binding(0)
resource: {
buffer: matrixBuffer, // buffer容器
offset: 0, // 数据偏移
size: 4 * 16 //数据大小
}
}
]
});
至此我们把数据捆成一个组了,接下来要传递到GPU里面
第五步:
pass.setBindGroup(0, bindGroup); //在每次draw之前调用
第六步:
const shadeCode = `
@binding(0) @group(0) var<uniform> matrix:mat4x4<f32>;
struct VertexOut {
@builtin(position) pos:vec4f,
@location(0) color:vec4f
}
@vertex
fn v_main(@location(0) pos:vec3f, @builtin(vertex_index) index:u32) -> VertexOut {
var out:VertexOut;
let i = f32(index);
out.pos = vec4f(pos, 1) * matrix;
let faceIndex = floor(i / 6);
var color:vec4f;
// 四方体不同面使用不同颜色绘制
if (faceIndex == 0) {
color = vec4f(1,0,0,1);
} else if(faceIndex == 1) {
color = vec4f(0,1,0,1);
} else if(faceIndex == 2) {
color = vec4f(0,0,1,1);
} else if(faceIndex == 3) {
color = vec4f(0.5,0.5,0,1);
} else if(faceIndex == 4) {
color = vec4f(0,0.5,0.5,1);
} else if(faceIndex == 5) {
color = vec4f(0.5,0,0.5,1);
}
out.color = color;
return out;
}
@fragment
fn f_main(@location(0) c:vec4f) -> @location(0) vec4f {
return c;
}
`
着色器代码的第一行就是读取了uniform变量,通过@binding和@group来取值,跟前面章节最大的逻辑区别是顶点着色器,其核心代码是out.pos = vec4f(pos, 1) * matrix,把坐标乘以矩阵得到新的坐标,也即是视角坐标(相机坐标)。vertex_index是WGSL的内部变量,表示顶点索引。我们通过顶点索引可以计算得出该顶点位于第几个面 floor(i / 6),因为每个面有六个顶点。之所以用if else是因为WGSL里面没有switch,也暂时没找到替代方法~还是if大法好走到哪都通用!。另外注意下WGSL里面没有三等,只有双等。片元着色器不变。
有个灵魂拷问:为什么matrix不直接在WGSL里面赋值,而要通过复杂流程绑定进来?因为matrix是个变量,只是暂时还没变,后面会让它变起来。你也可以在WGSL里面通过字符串拼接的形式动态写入变量,这样带来的后果是整个WGSL字符串为一个变量了。但是通过绑定的形式可以直接在CPU里面改变matrix的值再重新setBindGroup和draw即可改变图像而不需要重新解析WGSL字符串以提高性能。
三:配置管线
const pipeLineConfig = {
...
vertex: {
...
buffers:[
{
arrayStride: 12,
...
}
]
},
primitive: {
topology: 'triangle-list',
cullMode: 'back', // 背面不绘制
}
}
因为顶点坐标增加了z值这里arrayStride要加4个字节,从8变成12。topology使用三角形列表绘制模式(triangle-list)以及cullMode不渲染背面的顶点(back),其它配置不变,我用...省略了。
四:绘制动态3D
以上是绘制一个带有角度视角的立体图形,如果要绘制动态的,比如不断旋转的立体图,原理就是不断地改变视角计算得出该视角的matrix矩阵传入GPU,然后不断地draw就行了:
let rotation = 0;
function render() {
rotation += 0.02;
let rotateMatrix = createRotationMatrix(rotation, [-0.15, -0.95, 0]);
rotateMatrix = new Float32Array(rotateMatrix);
device.queue.writeBuffer(matrixBuffer,0,rotateMatrix.buffer,0,rotateMatrix.byteLength);
const encode = device.createCommandEncoder();
const pass = encode.beginRenderPass({
colorAttachments: [{
loadOp: "clear", //渲染前清空画布
clearValue: {r: 0, g: 0,b:0, a:1}, // 清空画布使用黑色覆盖
storeOp: "store", // 渲染后存储颜色配置
view: context.getCurrentTexture().createView() // 视图,使用此方法返回视图即可
}]
});
pass.setPipeline(pipeline); // 设置渲染管线
pass.setVertexBuffer(0, vertexBuffer); // 设置顶点buffer,偏移0,即从头到尾完整的数据
pass.setBindGroup(0, bindGroup);
pass.draw(allVertex.length / 3);
pass.end(); // 绘制完了要手动结束
device.queue.submit([encode.finish()]); // 指令编码器完成,提交到设备队列
requestAnimationFrame(render);
}
requestAnimationFrame(render);
这是自旋动画,你也可以通过鼠标事件开发人机交互的3D预览图。以下就是本章节的效果图,你学废了吗?

如果阅读本文有点吃力,建议先读通前面两章节文章,尤其是第一篇,包含了众多前置概念: